
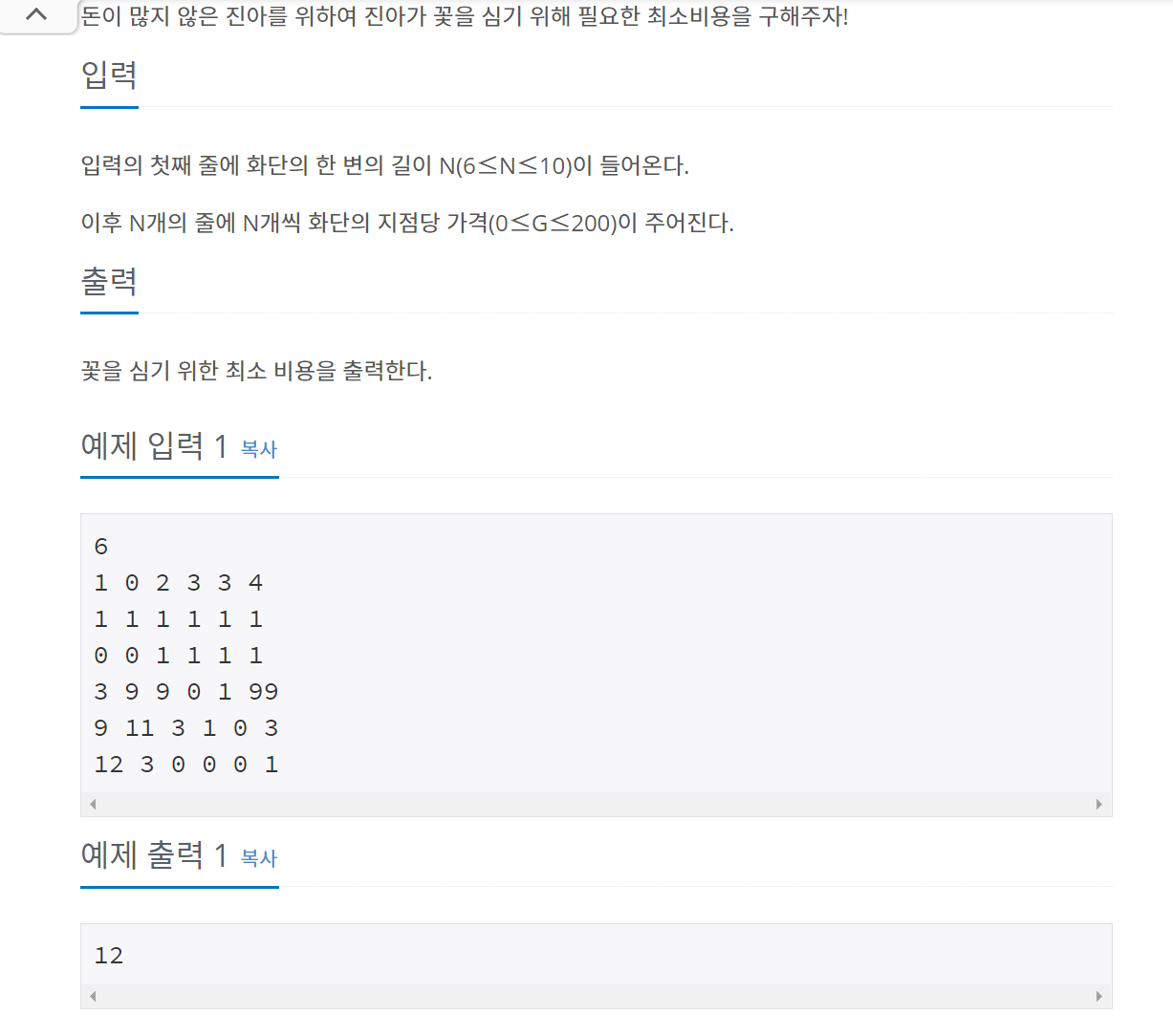
꽃을 하나 피우기 위해서는 위 그림의 (b) 모양 처럼 + 형태의 땅을 모두 빌려야하므로 최소 5칸을 빌려야한다.
거기에 꽃잎이 화단밖으로 나가면 죽고(?) 다른 꽃잎과 만나도 죽는다(개복치냐)
두 가지의 접근 방식이 필요하다.
하나는 특정 위치에 씨앗을 심을 경우 5칸의 비용이 얼마인지를 알아야한다.
또 하나는 꽃잎이 죽지 않는지를 판단해야한다.
나의 경우 (쓸데없이) 각 위치에서 비용이 얼마인지를 먼저 저장해놓고 그것을 토대로 Depth-First Search(DFS)
방식으로 접근한다.
#include<stdio.h>
#include<iostream>
#include<queue>
#include <algorithm>
using namespace std;
int Garden[11][11];
int Cost[11][11];
int Visited[11][11];
int dx[4] = {-1,1,0,0 };
int dy[4] = { 0,0,-1,1};
int Min = 9999999;
int cost(int y, int x) {
int ret = Garden[y][x];
ret += Garden[y + 1][x] + Garden[y - 1][x] + Garden[y][x + 1] + Garden[y][x - 1];
return ret;
}비용을 구하는 함수
화단의 크기 N이 최대 10 이므로 Cost[11][11] 배열의 크기를 11로 잡았다.
이후 cost(y,x) 함수를 수행하는데, 특정 위치를 주면 해당 위치와 상하좌우의 비용을 모두 더해 return 해준다.
바로 Cost[][] 에 저장하면 좋다.
cost()함수를 모든 지점에서 수행하되, 심을 수 없는 지역, 즉 화단 밖으로 꽃잎이 나가는 지역인 화단의 경계 지역에서는
수행하지 않도록 범위를 잘 잡아준다.(main함수 내 존재)
DFS는 깊이 우선 탐색으로 BFS와는 개념이 다르다.
앞선 글에서 BFS는 해당 시각에서 갈 수 있는 곳을 모두 후보로 집어넣고 나서 나중에 다시 꺼내서 살펴봤고,
같은 시각에 있는 다른 위치에서 길을 찾아 종료지점에 도착했는지 판단했다.
만약 도착하지 않았다면 시각이 단위만큼 증가하게 되고 그 시각에 존재하는 모든 지점에서 다시 살폈다.
하지만 DFS는 갈 수 있는 곳이라면 일단 가본다.
일단 계속 가서 종료지점까지 갈 수 있는지를 판단하고 없다면 뒤로 돌아온다.
만약 종료지점이라면 그 분기는 끝이 난다.
일반적인 탐색이라면 종료지점에 도착할 경우에 끝이 나게 된다.
하지만 가장 빠르게 종료지점까지 도착할 경우를 찾고 싶을 경우 모든 분기에 대해 수행하여
모든 경우를 다 살펴봐야한다.
BFS가 특정 시각에 도착하는 지를 살피고 도착한다면 바로 끝을 내는 것과는 사뭇 다르다.(시간을 단위로 증가)
내가 가려는 칸이 나보다 먼저 갔었던 경우가 있었다면 탐색하지 않는다.(탐색해도 항상 과거보다 늦게 가기 때문)
갈 수 있는 칸이 여러개라면 (평행우주마냥) 분기가 갈리고, 내가 정한 방향 순서대로 탐색을 각각 시행한다.
내가 정한 방향 순서는 그 자리에서 갈 수 있는 방향을 순서대로 탐색한다.
예를 들어 특정 위치에서 위로도 갈 수 있고 아래로도 갈 수 있다면, 내가 정한 방향 순서 상 아래가 먼저이므로
아래로 먼저 탐색한다.
모든 분기가 끝나면 종료한다.
쫄라맨의 모험 시작!

int DFS(int y, int x, int n, int num,int sum) {
//yx 위치, n 화단의 크기, num 꽃잎 심은 개수, sum 비용의 총합
//종료조건, 꽃잎을 3개 심었을 경우
if (num == 3) {
//3개 심은 곳의 비용이 내가 알고 있던 것보다 작다면 저장
// Min은 전역변수
if (Min > sum )
Min = sum ;
return 0;
}
//내가 심은 지점 저장
Visited[y][x] = 1;
//내가 심은 지점이 화단 경계 안쪽에 있고(main에서 범위제한)
//주변 + 모양까지 모두 꽃으로 바꿈.
for (int i = 0; i < 4; i++) {
int neary = y + dy[i];
int nearx = x + dx[i];
Visited[neary][nearx] = 1;
}
// 화단의 경계를 제외한 1~n-1 까지 탐색
// 중복되는 탐색이 많이 있어 시간이 증가하나 화단의 크기가 10x10 에 불과하므로 그대로 작성
for (int i = 1; i < n-1; i++) {
for (int j = 1; j< n-1; j++) {
//꽃잎이 없을 경우 그 자리 심어보기
if (!Visited[i][j]) {
int go = 1;
// 그 자리에 심었을 경우 다른 꽃잎과 겹치는지 조사
for (int k = 0; k < 4; k++) {
int neary = i + dy[k];
int nearx = j + dx[k];
//겹칠 경우 심지 않고 종료
if (Visited[neary][nearx]) {
go = 0;
break;
}
}
//겹치지 않을 경우 그 자리에 심고 다른 자리 DFS탐색
if (go) {
DFS(i, j, n, num + 1, sum + Cost[i][j]);
//그 자리를 DFS 탐색한 후 빠져나왔으므로 방문하고 있지 않다는 것을 저장하기 위해 0으로 초기화
Visited[i][j] = 0;
for (int k = 0; k < 4; k++) {
int neary = i + dy[k];
int nearx = j + dx[k];
Visited[neary][nearx] = 0;
}
}
}
}
}
//가장 초기에 심었던 위치도 방문점 초기화
Visited[y][x] = 0;
for (int i = 0; i < 4; i++) {
int neary = y + dy[i];
int nearx = x + dx[i];
Visited[neary][nearx] = 0;
}
return 0;
}중복되는 경우를 제외하면 실행시간이 조금 더 짧아질 수 있겠지만 고민하기 힘들어서 관뒀다.
모든 지점에 한 번씩 심어보고 그 때 가질 수 있는 Min 값을 계속해서 저장하고 갱신해간다.
메인함수에서는 입력받고 cost를 계산후 DFS를 수행한후 Min값을 출력한다.
int main() {
//입력
int n;
scanf("%d", &n);
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
scanf("%d", &Garden[i][j]);
}
}
// 각 위치별 비용 계산(경계제외 1~n-1)
int size = 0;
for (int i = 1; i < n - 1; i++) {
for (int j = 1; j < n - 1; j++) {
Cost[i][j] = cost(i, j);
}
}
// 각 위치에 하나 심고 나머지 두 개를 어디에 심는게 최소인지 구함(경계제외 1~n-1)
for (int i = 1; i < n - 1; i++) {
for (int j = 1; j < n - 1; j++) {
DFS(i, j, n, 1, Cost[i][j]);
}
}
printf("%d", Min);
}
DFS 하나로 풀 수 있는 문제지만 꽃잎이 겹치지 않게 탐색해야하는 조건이 추가된 유형인 것 같다.
자신이 방문함 지점과 꽃잎이 필 지점까지 전부 표시해두면 금방 풀 수 있다.
전체코드
#include<stdio.h>
#include<iostream>
#include<queue>
#include <algorithm>
using namespace std;
int Garden[11][11];
int Cost[11][11];
int Visited[11][11];
int dx[4] = {-1,1,0,0 };
int dy[4] = { 0,0,-1,1};
int Min = 9999999;
int cost(int y, int x) {
int ret = Garden[y][x];
ret += Garden[y + 1][x] + Garden[y - 1][x] + Garden[y][x + 1] + Garden[y][x - 1];
return ret;
}
int DFS(int y, int x, int n, int num,int sum) {
if (num == 3) {
if (Min > sum )
Min = sum ;
return 0;
}
Visited[y][x] = 1;
for (int i = 0; i < 4; i++) {
int neary = y + dy[i];
int nearx = x + dx[i];
Visited[neary][nearx] = 1;
}
for (int i = 1; i < n-1; i++) {
for (int j = 1; j< n-1; j++) {
if (!Visited[i][j]) {
int go = 1;
for (int k = 0; k < 4; k++) {
int neary = i + dy[k];
int nearx = j + dx[k];
if (Visited[neary][nearx]) {
go = 0;
break;
}
}
if (go) {
DFS(i, j, n, num + 1, sum + Cost[i][j]);
Visited[i][j] = 0;
for (int k = 0; k < 4; k++) {
int neary = i + dy[k];
int nearx = j + dx[k];
Visited[neary][nearx] = 0;
}
}
}
}
}
Visited[y][x] = 0;
for (int i = 0; i < 4; i++) {
int neary = y + dy[i];
int nearx = x + dx[i];
Visited[neary][nearx] = 0;
}
return 0;
}
int main() {
int n;
scanf("%d", &n);
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
scanf("%d", &Garden[i][j]);
}
}
int size = 0;
for (int i = 1; i < n - 1; i++) {
for (int j = 1; j < n - 1; j++) {
Cost[i][j] = cost(i, j);
}
}
for (int i = 1; i < n - 1; i++) {
for (int j = 1; j < n - 1; j++) {
DFS(i, j, n, 1, Cost[i][j]);
}
}
printf("%d", Min);
}
'알고리즘' 카테고리의 다른 글
| 백준 1707 이분 그래프 (0) | 2021.02.21 |
|---|---|
| 백준 11053 가장 긴 증가하는 부분 수열 C++ (0) | 2021.02.19 |
| 백준 2178 미로탐색 - C++ BFS (0) | 2021.02.12 |
| 백준 1747번 소수&팰린드롬 - C언어 (0) | 2021.02.12 |
| 백준2108 통계학 - C언어 (0) | 2021.02.09 |