1. 기초 논리회로
*주의 - 개인적으로 학습한 내용이므로 틀릴 수 있습니다. 잘못된 내용일 경우 알려주시면 진심으로 감사드리겠습니다.
가. 논리 게이트 Logic Gates
컴퓨터는 계산을 위해 전기적인 시스템을 이용한다.
연산에 쓰이는 회로 부품을 논리 게이트라고 부르는데,
일정한 수준의 전압 이상의 전압을 걸면 신호로 인식하는 부품이다.
예로 3V 이상의 전압을 신호로 인식하는 게이트를 사용하면,
3V 미만의 전압은 전기가 통하지 않게, 그 이상은 통하도록 만들어져 있다. (혹은 반대로 작동)
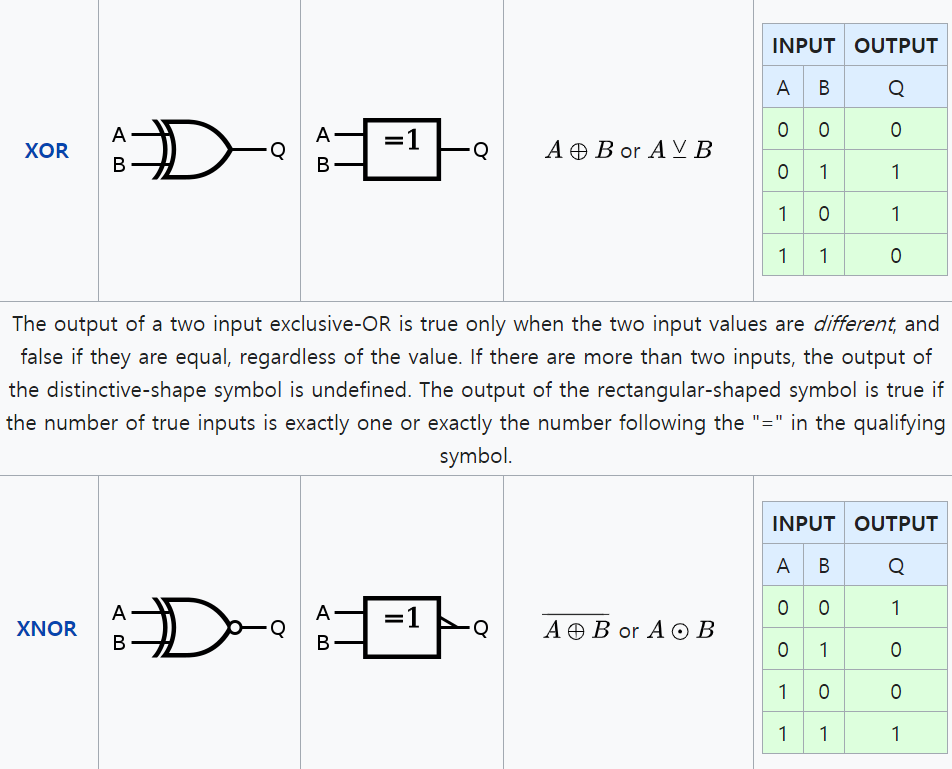
논리 게이트는 6가지를 사용하며,
1개를 제외한 나머지 5가지는 두 신호를 입력받아
정해진 규칙에 따라 신호로 내보낸다.
나머지 1개는 한 신호를 입력받아 그 입력을 반대로 뒤집어주는 역할을 한다.
전기 신호는 0V 나 5V로 양자화되어있고,
5V 면 전기 신호가 있다고 판단하여 1을 사용,
0V면 전기 신호가 없다고 판단하여 0을 사용한다.
실제로는 앞서 언급했듯이 일정 수준의 전압에 미치지 못하면
모두 0으로 처리하기 때문에, 어느 정도 수준의 노이즈를 없앨 수 있고,
반대로 전압이 부족할 경우 모두 0으로 처리되기 때문에
물리적으로 구현할 때는 신경을 써야 한다.
논리 게이트의 작동을 이해하기 위해 진리표(Truth table)를 작성하며,
진리표는 입력받은 신호와 출력되는 신호를 각각 기록한다.
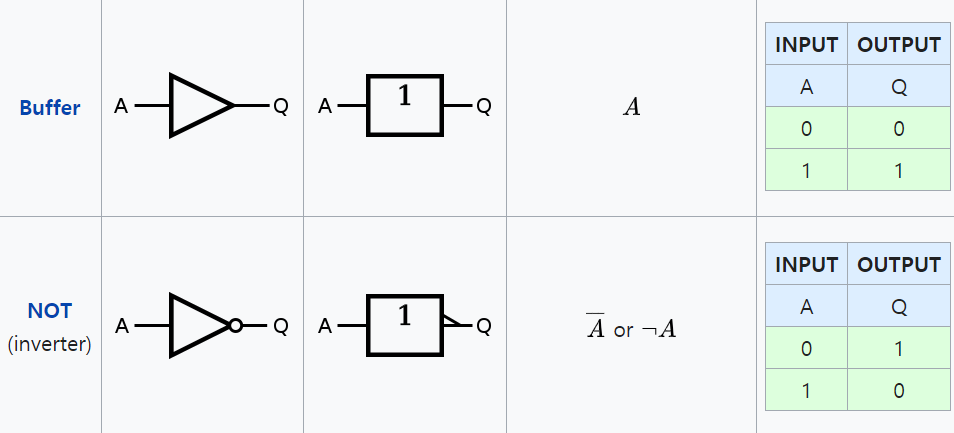

그림으로 몇 번 동작을 이해하다 보면 회로가 복잡해졌을 때
하나하나 눈으로 찾기 힘들 것이라는 생각을 하게 된다.
그래서 1854년 Boole 이 사용한 부울 대수(Boolean Algebra)를
사용하여 수학적인 기호로 결과를 예측한다.
증명은 진리표의 비교에 맡긴다.
(부울 대수 법칙 표와 특징, 증명은 진리표)
A의 부정(NOT) 은 A' 혹은! A 혹은 A bar로 표기하며, OR는 +, AND = * 로 정의한다.
일반적인 대수학과 차이가 있으니 주의해야 한다. (빨간 글자)
| MONOTONE LAWS (INPUT이 0->1 일 때 OUTPUT이 1->0 이 되지 않는 경우) | ||
| DOUBLE NEGATION | '('A) = A | |
| 논리곱의 IDENTITY, ANNIHILATOR |
0A=0 | 1A=A |
| 논리합의 IDENTITY, ANNIHILATOR |
0+A=A | 1+A=1 |
| 논리합의 IDEMPOTENCE | A+A = A | AA=A |
| 교환(COMMUTATIVITY) | AB=BA | A+B=B+A |
| 결합(ASSOCIATIVITY) | (AB)C=A(BC) | (A+B)+C= A+(B+C) |
| 분배(DISTRIBUTIVITY) | A(B+C) = AB+AC | A+BC = (A+B)(A+C) |
| 흡수(ABSORPTION) | A(A+B) = A | A+AB = A |
| NONMONOTONE LAWS | ||
| 부정(COMPLEMENTATION) | AA'=0 | A+A'=1 |
| 드모르강(DE MORGAN) | (AB)' = A' + B' | (A+B)' = A'B' |
위의 회로를 부울 대수로 정리한 결과는 다음과 같으며,
처음 작성한 진리표와 비교할 시 똑같은 결과를 얻을 수 있는 것을 확인할 수 있다.
요즘은 여러 개의 논리 게이트가 함께 들어있는 IC칩을 실험에 사용하며,
보통 4~8개의 게이트가 한 칩에 담겨 있어 좁은 공간에 활용이 가능하다.
이 논리 게이트의 기본적인 작동 방법을 파악했다면,
이 전기신호와 게이트들을 이용하여 연산이 가능함을 알 수 있다.
가령 덧셈을 할 경우, 0과 0이 들어올 때 0, 0과 1이 들어올 때 1,
1과 1이 들어올 때 2( 10 ) 임을 생각해 보면,
이진수의 첫자리가 둘 중 하나만 1이면 결과가 1,
둘 다 0 이거나 둘 다 1일 경우 결과가 0 임을 알 수 있으므로
XOR 게이트를 사용하는 것을 알 수 있다.
이 간단한 생각을 회로로 설계하면 다음과 같다.
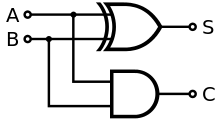
XOR 회로로 두 신호가 서로 다를 때 S에 1이 저장된다.
AND 회로로 둘 다 1이면 C에 1이 저장된다.
결과는 같은 자릿수의 계산 (0 + 1 = 1)인 SUM과
위의 자릿수로 올라가는 (1+1 = 10(이진수)) CARRY로 나누어 생각한다.
즉, 자릿수가 올라갈 경우 CARRY 가 유의미한 신호를 내보내고,
둘 중 하나만 1일 경우 SUM 이 유의미한 신호를 내보내 자릿수 여부와 합계까지 전기신호로 알 수 있다.
그리하여 자릿수마다 SUM을 저장하고(메모리에) CARRY를
다음 덧셈에 신호로 합성시킨다면 덧셈을 수행할 수 있다는 것을 생각할 수 있는데,
여기서 문제가 발생한다.
그림에서 보듯, CARRY의 신호가 다음 Half Adder에 들어갈 자리가 없다.
그러므로 사실상 1+1까지의 계산만을 수행할 수 있고,
그 위의 자리, 즉 10 + 10 등은 수행하여도 똑바로 계산할 수가 없다는 것을 의미한다.
그렇기 때문에 CARRY를 다음 덧셈에 반영할 수 있는 다른 방식의 필요성이 대두된다.
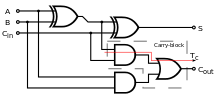
그림을 보면 알겠지만, Half Adder의 확장판이다.
첫 번째 Half Adder의 결과가 SUM1과 CARRY1에 저장되고,
저번 덧셈에서 넘어온 CARRY2를 SUM1에 더한다.
더하여 첫 번째 자릿수의 결과가 SUM2에 저장되고,
첫 번째 덧셈에서 발생한 CARRY1과 두 번째 덧셈에서 발생한 CARRY2 중
하나라도 CARRY 가 있다면 1의 신호로 바꿔주는 OR 게이트가 추가됐다.
이때, CARRY는 최대 1번만 발생할 수 있기 때문에 OR 게이트로 처리한다고
생각하면 편하게 이해할 수 있다.
가령 x y z 가 각각 1 1 1 일 때 최대인데,
각자 더하면 CARRY는 한 번 밖에 발생하지 않기 때문임을
생각하면 OR 게이트를 쉽게 이해할 수 있다.
이 Full Adder를 직렬로 쭉 연결하면 덧셈기가 완성되며,
8개 연결하면 SUM1 ~ SUM8까지 나오는 8비트 덧셈 계산기를 만들 수 있다.
하지만 직렬로 연결된 만큼 자릿수 순서대로 계산을 하기 때문에
숫자가 커질 경우 상당한 시간을 요구한다.
지금까지 INPUT 이 많아야 3개인 회로를 계속해서 다뤘다.
그럼에도 불구하고 회로가 길어지거나 복잡해질 경우 회로를 설계하기는 쉽지 않다.
여기서 MAURICE KARNAUGH 가 만든 MAP을 이용하면
INPUT 이 많게는 5개까지 들어오는 회로를 진리표를 활용하여 쉽게 설계할 수 있다.
다이아그램의 변형인 형태로, 진리표를 만든 후에
그것을 부울 대수로 표현할 수 있게 도와주는 MAP이라 생각하면 된다.
(혹은 분석하는 데 사용하거나)
지금은 거의 쓰이지 않고 HDL을 사용한다고 하지만,
초기에 어떤 식으로 설계하고 분석했는지 시도해보고 싶다면 WIKIPEDIA를 참고하길 바란다.
Karnaugh map - Wikipedia
Karnaugh map - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search graphical method to simplify Boolean expressions The Karnaugh map (KM or K-map) is a method of simplifying Boolean algebra expressions. Maurice Karnaugh introduced it in 1953[1][2] as
en.wikipedia.org
간단하게 생각하면, 진리표를 만들고,
숫자 순서대로 네모난 표에 집어넣은 다음 2의 배수(1,2,4,8,..)의 단위로
인접한 블록들을 묶는 것이다.
A에 속하면 A를 붙이고 B에 속하면 B를 붙이는 식으로
모든 박스를 부울 대수로 표현할 수 있는데,
가장 간단한 형식으로 만들고 싶다면 크게 크게 박스를 묶으면 된다.
(쉬운 이해를 위해서 WIKIPEDIA의 2-variable map examples를 참고하면 좋다.)
예를 들어 INPUT 이 3개인 진리표가 다음과 같이 생겼다면
| INPUT A | INPUT B | INPUT C | OUTPUT Z |
| 0 | 0 | 0 | 0 (0번째) |
| 0 | 0 | 1 | 1 (1번째) |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 (7번째) |
KARNAUGH MAP 은 순서에 따라서(괄호로 표시)로 작성한다.
| B | B | |||
| 0(0번째) | 1(1번째) | 0 (4번째) | 0 (3번째) | |
| A | 1 (4번째) | 1 (5번째) | 1 (7번째) | 0 (6번째) |
| C | C |
여기서 A B C에 해당하는 블록들을 부울 대수로 ABC로 표현할 수 있고,
해당하지 않는다면 A' B' C'로 표현한다.
여기서 1인 블록끼리 근접했을 경우(반대편으로 넘어가도 괜찮다) 2의 배수 개수로 묶는다.
가령 이 경우는 3가지로 묶을 수 있는데,
빨간 배경 글자 (1번째 5번째), 기울어진 글자(4번째 5번째), 보라색 글자(5번째 7번째)를
2개씩 3묶음으로 표현할 수 있다.
빨간 배경 글자부터 표현하면, B'과 C의 공통 영역에 있고
A 와는 관계없으므로(A와 A' 둘 다 가능) B'C로 표현이 가능하다.
기울어진 글자는 B'과 A의 공통영역이므로 AB'으로 표현한다.
보라색 글자는 A와 C의 공통영역이므로 AC로 표현한다.
이렇게 위의 진리표는 Z= AB' + B'C + AC로 표현할 수 있다. (진리표로 확인 가능)
나. 조합 회로(Combinational logic)와 순차 회로(Sequential logic)
지금까지의 기초 회로들은 INPUT 값에만 의존하여 OUTPUT에 나오는 회로였다.
하지만 과거의 상태가 현재의 OUTPUT의 영향을 주는 회로가 있다.
전자를 조합 회로, 후자를 순차 회로라고 명칭 한다.
지금까지는 조합 회로를 살펴봤으니 이제 순차 회로를 살펴본다.
복잡한 회로는 (배우지 않았으므로) 넘어가고
이 글에서는 SR Latch와 Flip-Flop을 살펴보기로 한다.
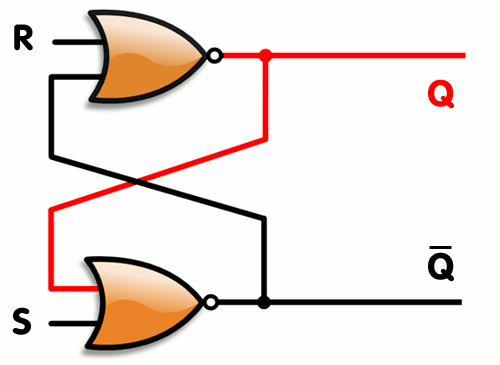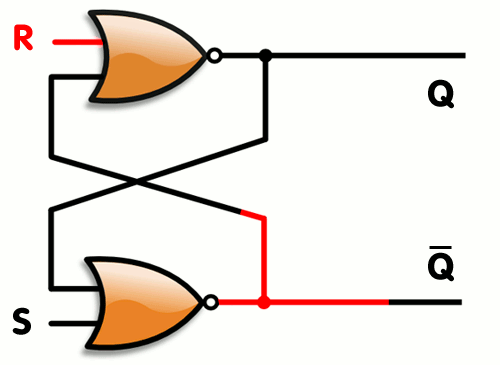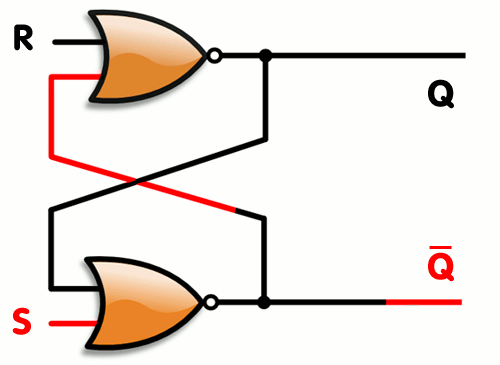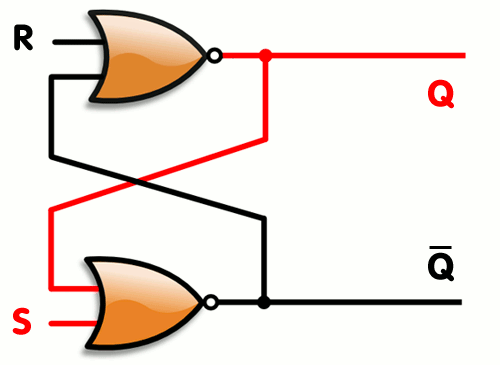
SR latch는 말 그대로 S와 R이 서로 걸려있는 것을 의미한다.
과거에 진행되었던 논리가 다시 다른 쪽의 INPUT으로 들어가기 때문에 현재의 상태에 영향을 끼친다.
SR latch 에는 두 개의 NOR 게이트가 사용되는데,
앞서 언급했듯 둘 다 0일 일 때만 신호가 나온다.
이것을 진리표로 표현하면 다음과 같다.
이때 첫 상태는 Q=1 , Q bar =0으로 가정한다.
| S | R | Q | Q bar |
| - | - | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 |
| 1 | 1 | ? | ? |
보이는 바와 같이 Q에 1, Qbar에 0이 걸려있다면
S에 어떤 값이 들어오든 항상 신호는 0이 나온다.
하지만 R에 1이 들어올 경우 Q의 전류가 끊기면서 S 가 0이면 신호가 나올 수 있다.
반대로 Q가 0, Qbar에 1의 경우, S가 1이어야만 신호가 끊기고, R에 0이 와야만 Q에 신호가 들어간다.
S R 이 둘 다 1인 경우를 제외하고,
S에 1을 넣으면 Q가 1 Qbar가 0, R에 1을 넣으면 Q가 0 Qbar가 1이 들어가는 것을 볼 수 있다.
그렇기 때문에 우리가 사용하는 메모리가 Q 일 경우 S를 Set,
R을 Reset이라고 부른다.
그리고 둘 다 0일 경우 과거의 OUTPUT을 유지한다.(LATCH)
단, 여기서 S와 R이 둘 다 1일 경우 문제가 발생한다.
둘 다 1이 들어올 경우, 양쪽의 신호가 끊기므로
Q와 Q bar 가 0이 되어버려 저장되었던 내용이 사라져 버린다.
그렇기 때문에 금지된 입력(Inhibit Input)으로 부르며 사용 시에 항상 주의를 기울여야 한다.
하지만, 주의를 기울여서 사용해도 전기신호의 주파수가 올라가면 물리적인 제한이 따른다.
가령 INPUT 전기를 주는 SOURCE의 전압을 높이는 속도와 낮추는 속도가 다를 경우,
S와 R에 동시에 신호를 변화시켜도 어느 한쪽이 더 빠르게 입력될 수 있다.
혹은 순간적으로 노이즈가 신호로 인식될 수 있다.
이럴 경우 금지된 입력이 될 가능성이 매우 높아지므로
조금 더 안전한 또는 금지된 입력이 없는 LATCH 가 필요하다.
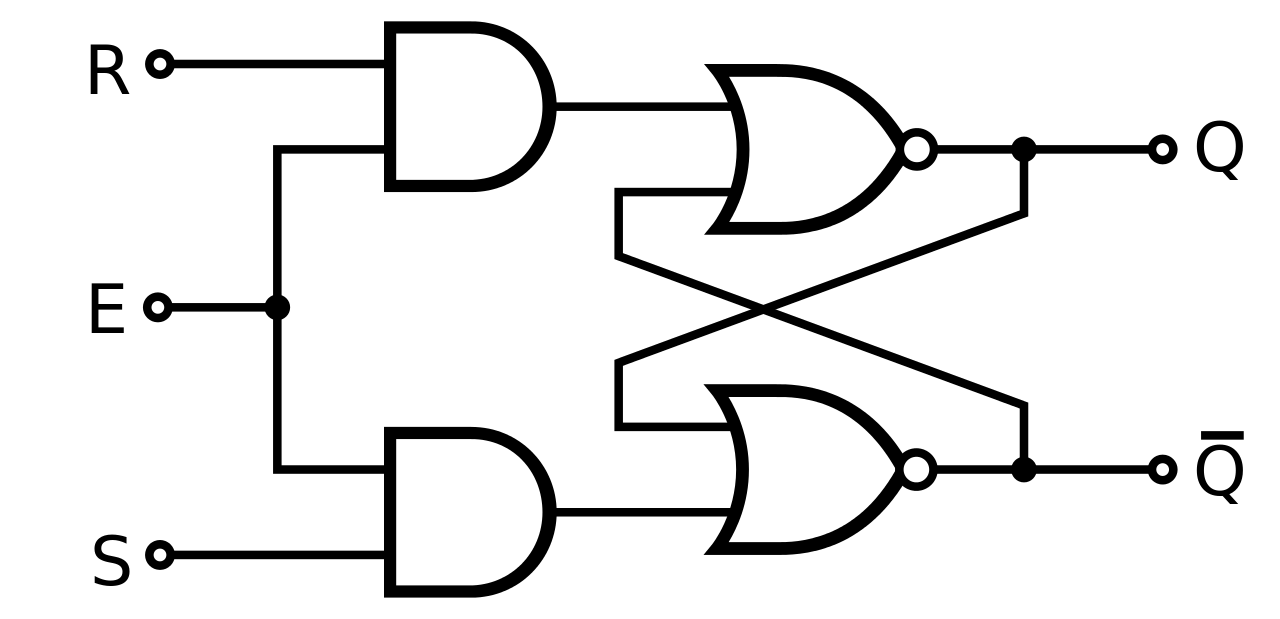
이 그림은 SR LATCH의 입력의 안정성을 위해 S와 R에 AND GATE를 추가하고
둘을 동시에 제어하기 위한 ENABLE SOURCE 가 추가된다.
E의 신호가 0이면 항상 입력이 0이 되므로 과거의 OUTPUT이 유지되고,
E의 신호가 1일 경우에만 S와 R의 신호가 입력될 수 있다.
내가 입력하고 싶은 S와 R 신호를 미리 주고 있어도
E에 신호를 줄 때만 작동하므로 전압의 변화 속도와 노이즈로부터 안전해질 수 있다.
E가 1일 때 입력, 0일 때 비 입력인 회로를 LATCH라고 부르고,
E가 1->0 혹은 0->1로 변할 때 값을 변경하는 회로를 FLIP-FLOP이라고 부른다.
금지된 영역에 대해서도 사용할 수 있는 JK FLIP-FLOP (1 1 일 때 현재 출력을 반전시킴)
혹은 D FLIP-FLOP (1 1 일 때 유지) 등이 있고,
회로에 PRESET과 CLEAR 신호를 입력할 수 있게 만들어
강제로 Q=1 혹은 Q=0으로 만들 수 있게 한다. (Flip-flop (electronics) - Wikipedia 참고)
이러한 논리회로를 이용하여 산술 연산 장치(ALU : ARITHMETIC LOGIC UNIT)를 만들 수 있다.
숫자(자료 OPERAND)와 연산 동작 코드(OPCODE) ,
연산의 결과 (STATUS, 0이나 음수, CARRY 등)를 가지고 연산을 수행한다.
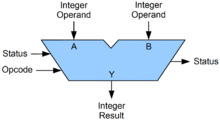
2개의 수를 INPUT으로 받아 하나의 OUTPUT을 내며 STATUS를 추가적인 정보로 제공한다.
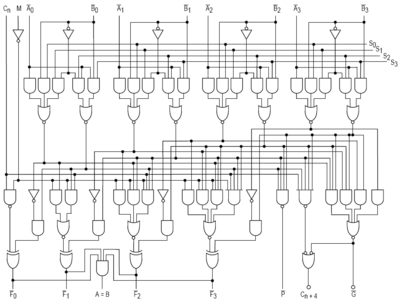
실제 ALU는 저런 구조의 회로를 여러 개 반복하여 제작하며,
위의 회로도의 경우 4BIT의 OUTPUT을 가짐을 볼 수 있다.
또한 명령에 따라 다른 연산을 수행하게 되는데,
제작 시에 정해둔 규칙에 따라 움직인다. (en.wikipedia.org/wiki/74181 참고)
ALU 옆에는 ALU의 연산에 쓰이는 데이터를 저장하는 공간인 REGISTER 가 있고,
이 둘을 제어할 수 있는 전기적 회로들을 CU : CONTROL UNIT이라 부른다.
세 가지를 합쳐 CPU : CENTRAL PROCESSING UNIT으로 부르며
DATA PATH를 따라 DATA BUS를 통해 프로그램과 메모리와 통신하여 필요한 연산을 수행한다.

탄도 계산을 위해 개발된 초기의 컴퓨터 애니악(1946)은 진공관 1만 8천여 개와
릴레이 1500개가 사용되어 길이만 약 25M에 달하는 거대한 기계였는데,
전자공학의 발달로 손바닥보다 작은 칩에 애니악보다 훌륭한 성능을 담기 시작하면서
CPU를 MICRO PROCESSOR로 부르게 되었고,
CPU+ 입출력 장치를 MICRO CONTROLLER
또는 SYSTEM ON A CHIP(SOC)라고 부르게 되었다.
CPU를 보면, 위의 논리회로가 그대로 쓰이게 되는데
(물론 조금 더 집적되거나 PIPELINE 등의 기능이 생겼겠지만),
ENABLE SOURCE에 해당하는 CLOCK에 동기 되어 연산을 수행, 저장하게 된다.
그리하여 요즘의 CPU (예를 들어 INTEL I5- 9600K 라던지)의 CLOCK 이
3.1 GHz라는 등의 주파수가 CPU 연산 속도를 파악할 수 있는 중요한 지표가 되었다.
다만 전기신호가 빛의 속도로 전파된다 해도 빛의 속도는 3 * 10^10 cm/s이고
GHz는 1*10^9 per sec 이므로 GHz 단위에서는 1초에 최대 30cm를 갈 수 있다.
만약 3 GHz 이면 1초 10cm이며 DDR(Double Data Rate) RAM을 사용할 경우
주파수의 두 배의 신호를 입출력하므로 1초에 5cm가 한계치이다.
이 말은 RAM과 CPU가 5cm 이상 떨어져 있으면 3 GHz 정도 스케일에서는
온전하게 데이터를 입출력하기 힘들 수 있다는 뜻이고,
이것이 물리적인 속도의 한계로 나타나고 있다.
그리하여 컴퓨터에서는 아직 CPU와 RAM이 멀리 떨어져 있어서 힘들지만,
휴대폰의 경우 적층 구조로 설계하여 효율을 높이고 있다고 한다.
하드웨어를 직접 제어하려면 DEVICE DRIVER를 다뤄 접근할 수 있고,
직접 하드웨어를 다루거나 고려하지 않고 편하게 다루기 위한 OS : OPERATING SYSTEM과
OS에서 지원하지 않는 기능을 지원해 주기 위해 OS위에서 개발한 API,
그리고 API와 OS를 이용하여 응용 프로그램(APP)을 만드는 것이 소프트웨어가 하는 일이다.
이렇게 하드웨어와 소프트웨어가 같이 있는 것을
임베디드 시스템(EMBEDDED SYSTEM)라고 부르며(PC제외) OS가 없을 경우 FIRMWARE라고 부른다.
'C언어' 카테고리의 다른 글
| C언어의 기초 - 포인터 (0) | 2021.02.06 |
|---|---|
| C언어의 기초 - 구조체와 공용체 (0) | 2021.02.03 |
| C언어의 기초 - 변수와 배열 (0) | 2021.02.03 |
| C언어의 기초 - 함수와 조건문, 반복문 (0) | 2021.02.01 |
| C언어의 기초 - 변수와 상수 (0) | 2021.02.01 |