알고리즘에서 정렬은 엄청나게 강력한 도구 중 하나이다.
하지만 비슷한 색의 공을 수만개를 한 번에 정렬하려고 하면 어떨까?
마치 퍼즐을 안쪽에서부터 맞추는 것처럼 엄청나게 어려울 것이다.
이를 위해 우리가 평상시에 어떤 정렬법을 사용하는지, 조금 더 빠른 정렬은 어떤 방식으로 진행되는지 공부한다.
log 수준으로 빠르게 작동하는 정렬법은 선형 자료구조를 마치고 다룬다.
1. 버블 정렬 Bubble sort
가장 쉽게 떠올릴 수 있고 개념도 직관적이며 이름마저 귀여운 버블 정렬이다.
마치 버블이 떠오르듯 차례대로 비교하며 가장 이해하기 쉽다.
하지만 O(N^2)의 수행시간을 반드시 가진다.
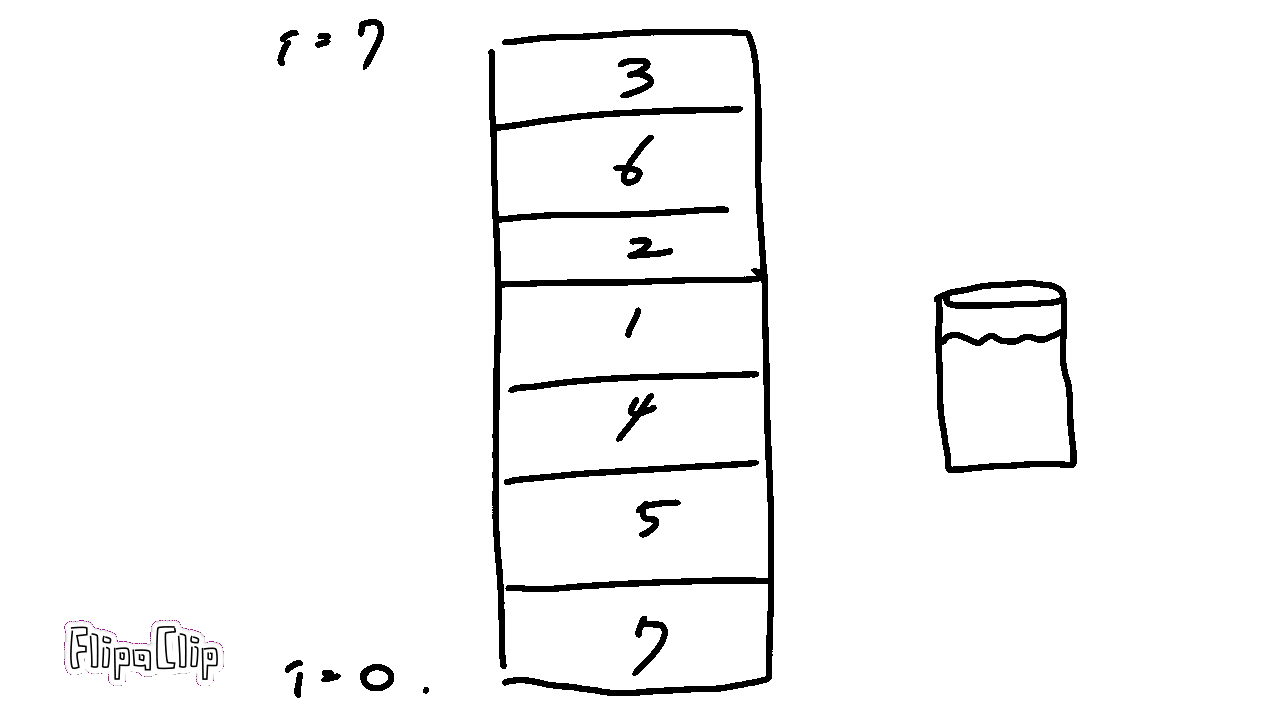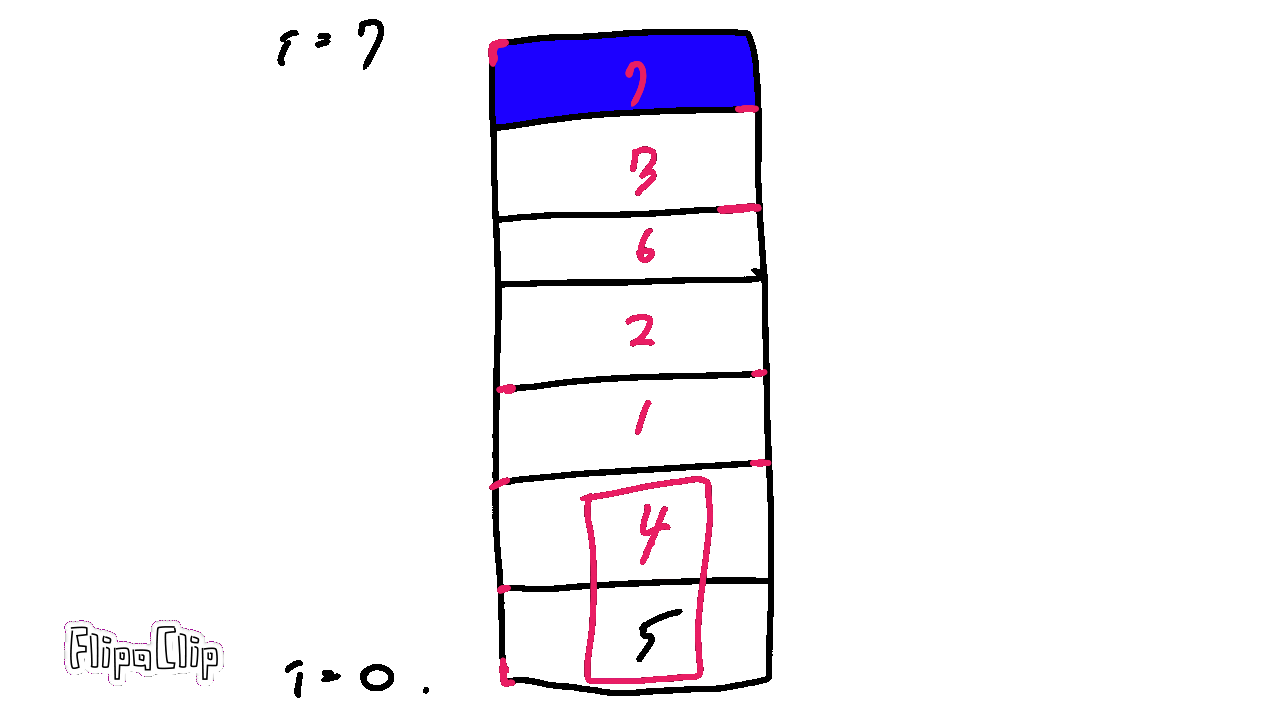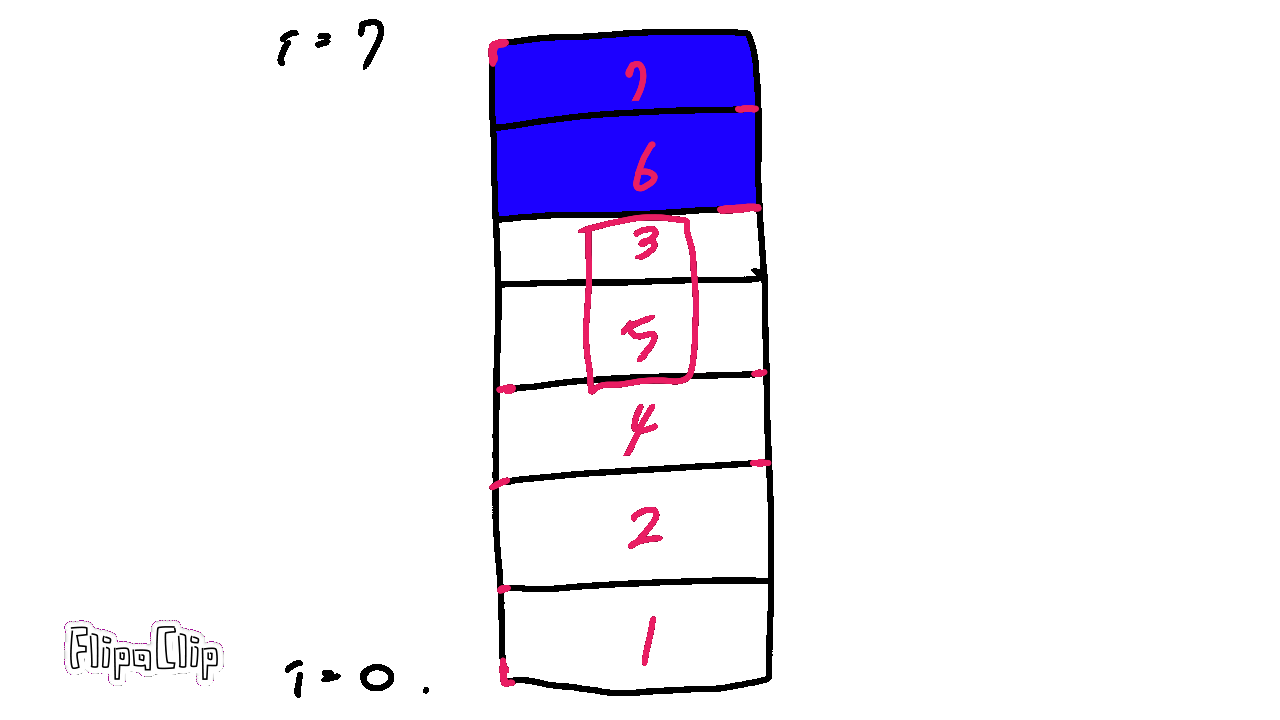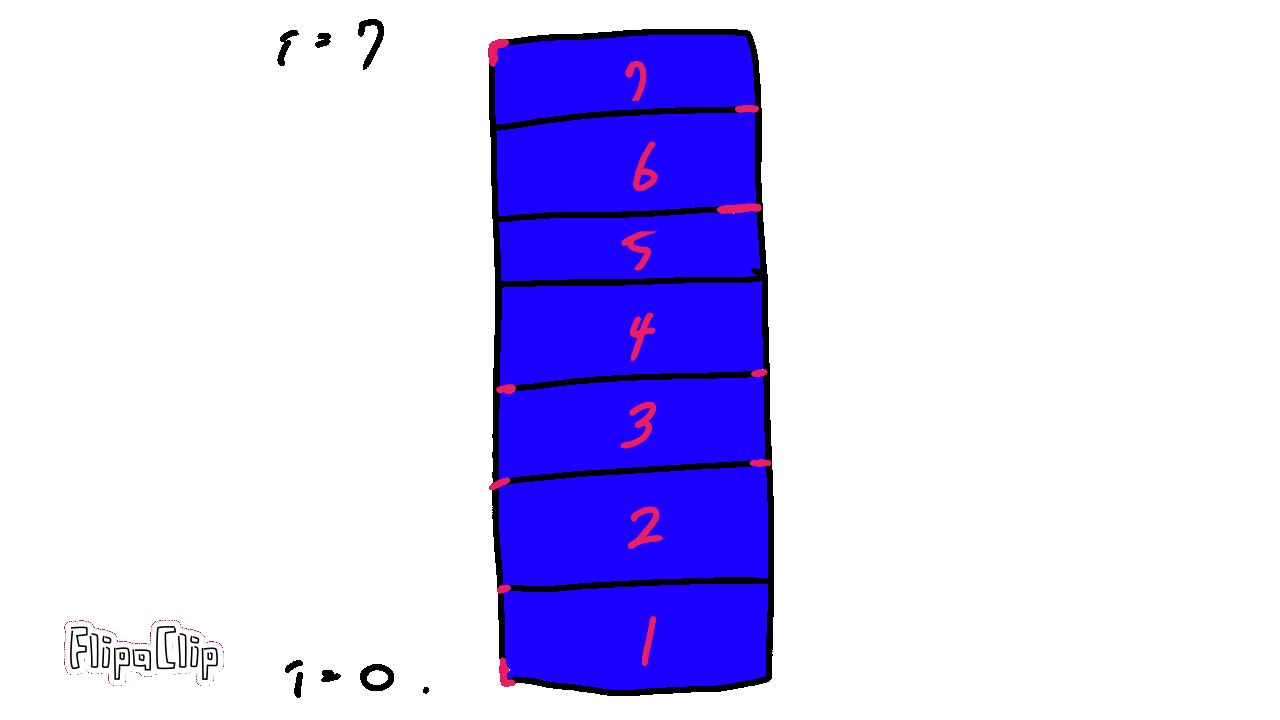
거품이 올라가듯 차례대로 스왑하는 것이 특징이다.
한 번 끝까지 올라갈때마다 최대수가 끝에 정렬되므로, i번 반복할 때 비교횟수는 n-1-i 번이 된다.
여기서 배열은 0으로 초기화되어 있고, 멤버는 0을 가지지 않는다고 가정하여 len 을 구했다.
int compare(int x, int y){
if (x>y) return 1;
else if (x==y) return 0;
return -1;
}
int Sort_Bubble(int * d, int order, int (*comp)(int x, int y))
{
//배열 d의 길이 구하기
int len = 0;
while (*d[len++]);
len -= 1;
// j번째와 j+1번째 비교, len 번 반복 (len-1번 반복이 맞지만 편의상)
for (int i = 0; i < len; i++) {
for (int j = 0; j < len - 1 - i; j++) {
//비교함수 기준으로 1이면 j가 크고 -1이면 j+1이 큰 값을 내보내므로 order 를 1,-1로
//설정하여 오름차순, 내림차순을 정할 수 있다. 1일 때 오름차순
if ( comp(d + j, d + j + 1) == order) {
int tmp = d[j];
d[j] = d[j + 1];
d[j + 1] = tmp;
}
}
}
return len;
}
버블함수의 기본 틀은 위와 같다.
개념은 그림과 완전히 동일하며, 함수를 호출하여 사용하는 call-back function의 개념을 사용했다.
order 에 따라 오름차순, 내림차순을 정할 수 있다.
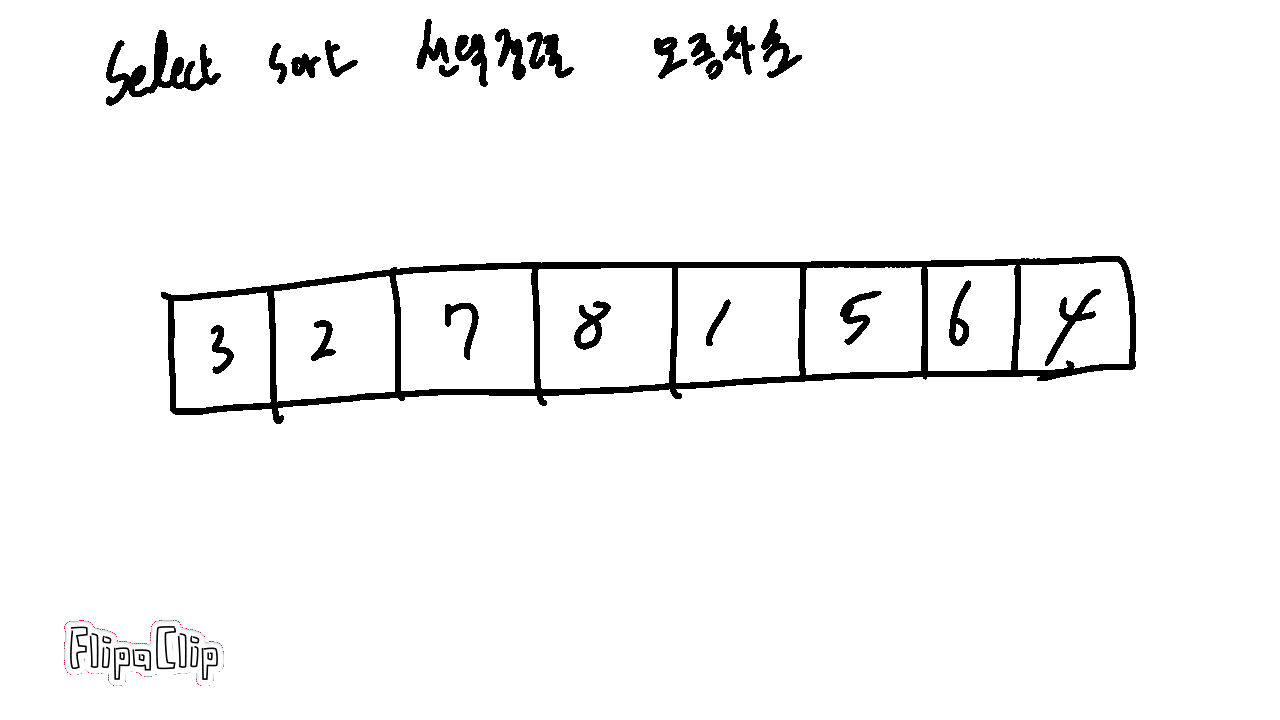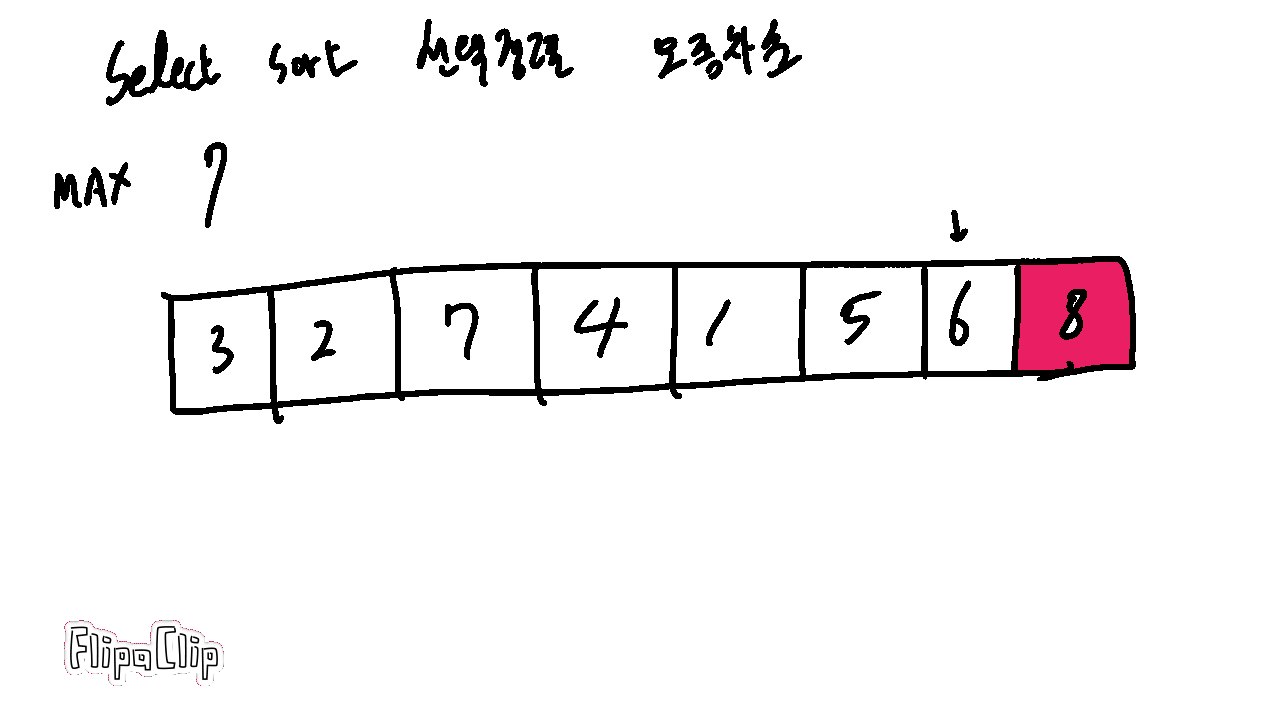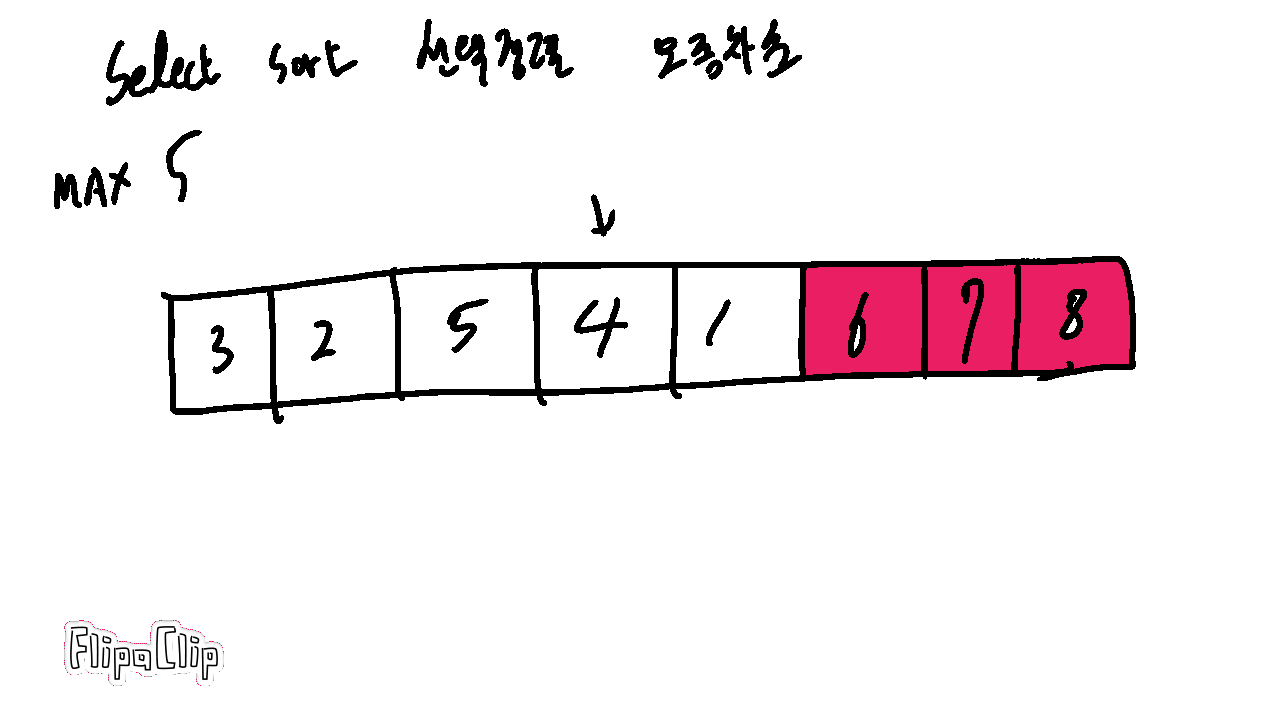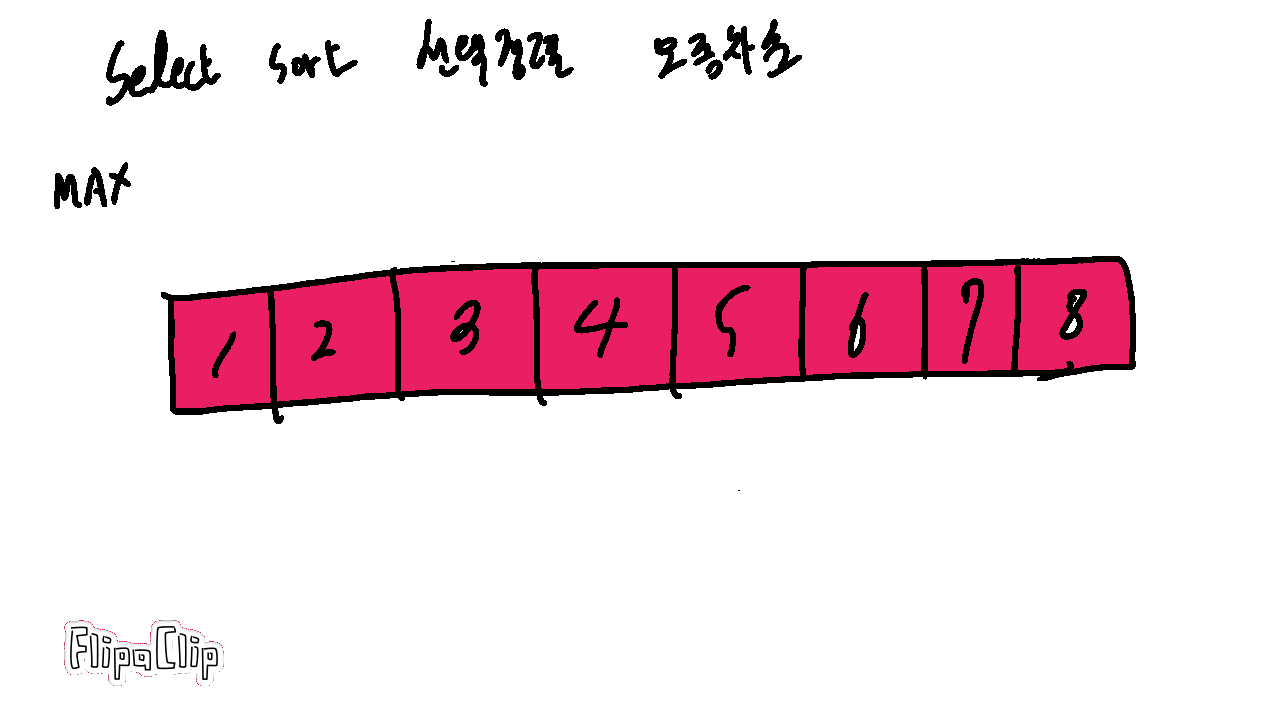
1-1. 선택정렬 Select Sort
버블 정렬이 모든 경우에 다 비교하고 스왑하는 것은 잠깐 생각해도 비효율적이다.
하지만 가장 큰 값이 한 번 수행할 때마다 가장 끝에 정렬되는 것을 조금 효율적으로 구현할 수 있다.(오름차순)
가장 큰 값을 따로 기억해두고 정렬을 훑을 때마다 끝에 저장하면 된다.
이럴 경우 스왑하지 않아도 되어 런타임에 이득이 있다.
int Sort_Select(int * d, int order, int (*comp)(int x, int y))
{
int len = 0;
while(*d[len++]);
for (int i = 0; i < len-1; i++) {
int tmp=d[0];
int maxidx = 0;
for (int j = 0; j < len-1 - i; j++) {
if ( comp(d[j],tmp) == order) {
tmp = d[j];
maxidx = j;
}
}
d[maxidx] = d[len-1-i];
d[len-1-i] = tmp;
}
return len;
}
2. 삽입 정렬 Insertion Sort
삽입 정렬은 초등학교 때 키 순서대로 줄을 세우는 것을 생각하면 편하다.
아무나 데리고 와서 이미 서있는 아이들을 기준으로 보다 크면 뒤로 작으면 앞으로 줄을 세운다.(오름차순)
개념자체가 새로운 아이들을 계속 데려와 세우는데 편리하다는 것을 알 수 있는데,
이미 정렬된 배열에 요소를 넣을 때 사용하면 좋다.
너무 익숙한 개념이기에 굳이 그림을 그리지 않았다.
int Sort_Insertion(int * d, int order, int (*comp)(int x, int y))
{
int len = 0;
while(*d[len++]);
len-=1;
//배열에서 숫자 뽑기
for (int i = 1; i < len; i++) {
//뽑은수 전까지 비교하면서 자리 찾기
int j = 0;
int tmp=d[i];
for (j = 0; j < i; j++) {
if (comp(d[j], d[i]) == order) {
break;
}
}
//자리 이후의 숫자들 다 밀기
for (int k = i; k > j; k--) {
d[k] = d[k - 1];
}
d[j] = tmp;
}
return len;
}논리는 위와 같다.
숫자를 뽑고 (len-1 번 뽑아야 항상 정렬이 된다.) 배열에서 숫자를 비교하며 자기보다 큰 숫자가 나오면(오름차순)
나머지 숫자를 모두 뒤로 밀어내고 그 자리에 숫자를 넣는다.
나머지 숫자를 밀어내기 때문에 배열의 크기는 항상 길이+1 보다 같거나 커야 오류가 없다.
배열에서 앞의 숫자부터 밀어내면 뒤의 숫자가 사라지기 때문에 뒤의 숫자부터 밀고 차례대로 앞으로 온다.(k)
3. 빠른 정렬 Quick Sort
stdlib.h 헤더를 사용한다면 아마 c에서 가장 애용될 Sorting 방법이다.
말 그대로 빠른 정렬 속도를 자랑하는데, 최악의 경우 버블 정렬과 다를 바 없이 수행되지만,
최선의 경우 자신보다 큰 수와 작은 수를 반씩 나누며 진행되기 때문에 log2의 수행시간을 따를 것이다.
기본 개념은 다음 그림과 같다.
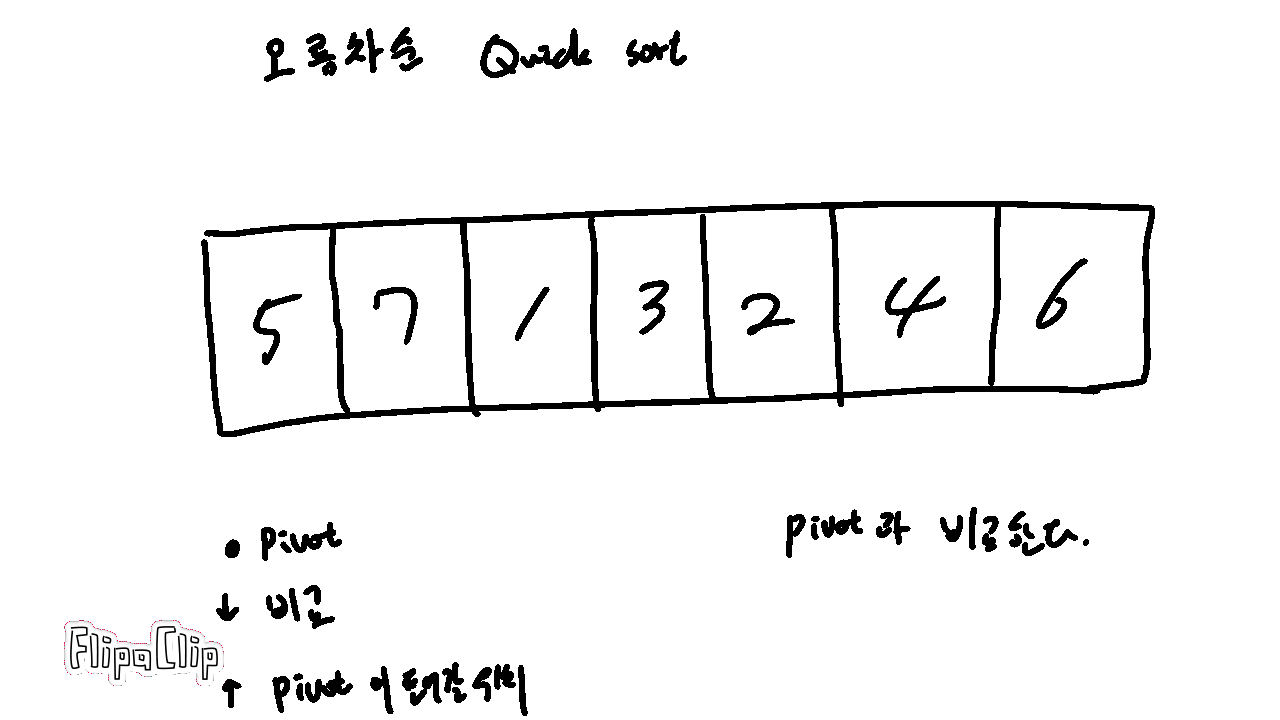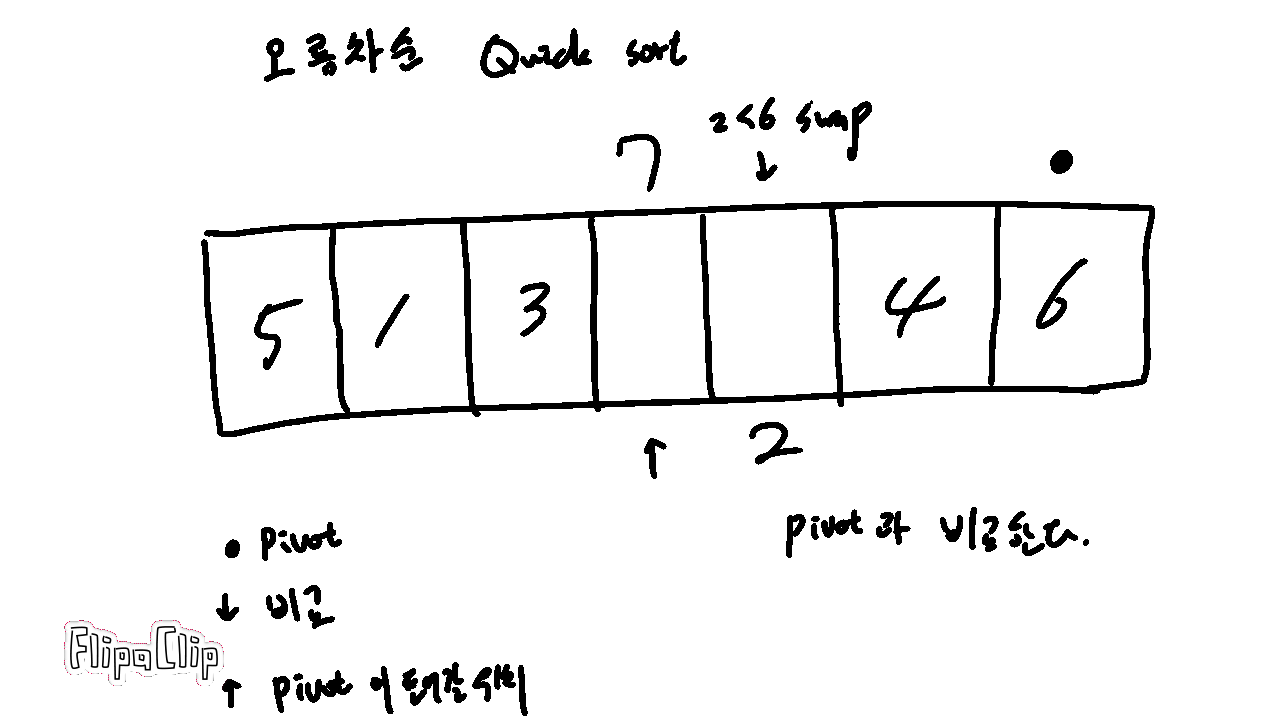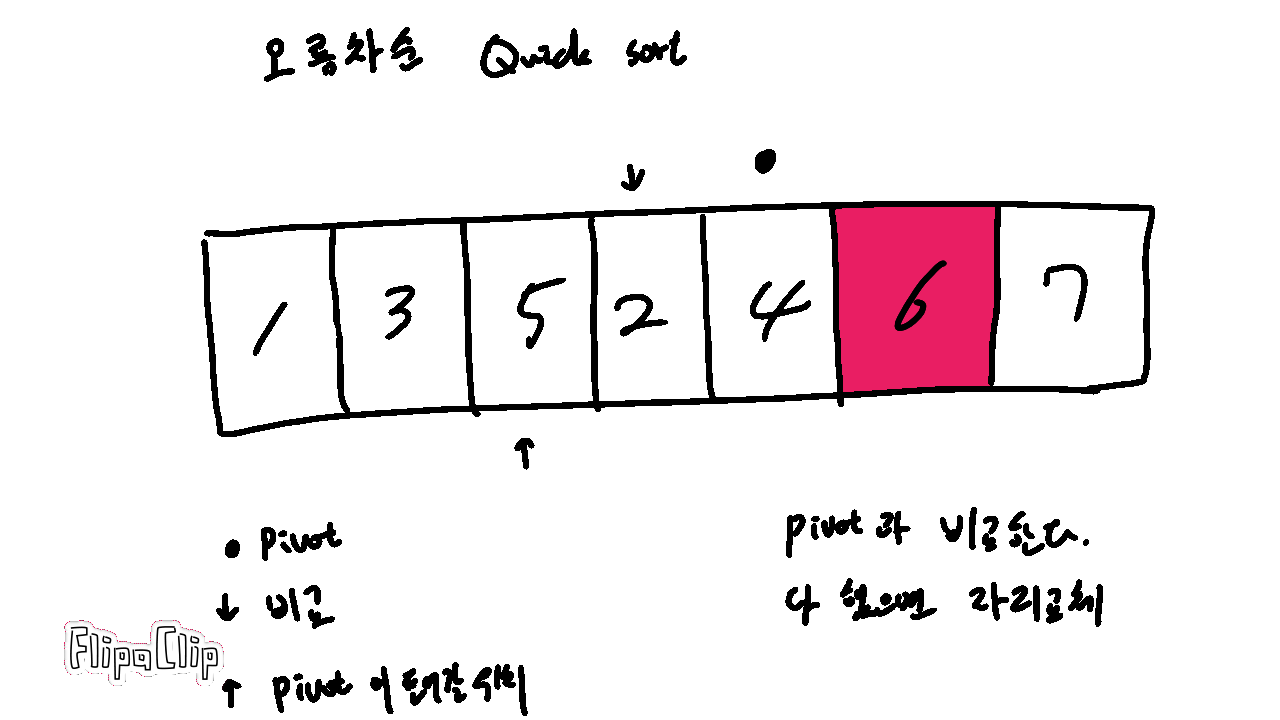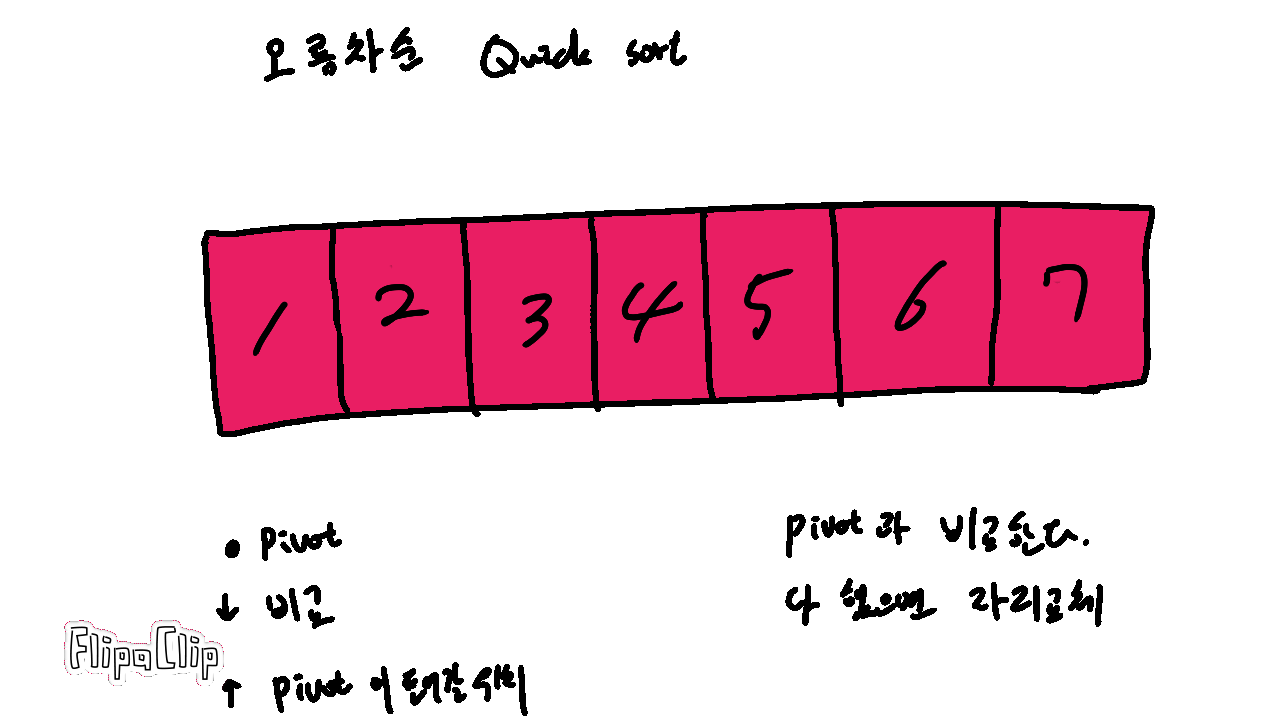
Pivot 은 기준이 되는 숫자를 의미한다.
현재 보는 위치는 Pivot 과 비교 중인 숫자를 의미한다.
Pivot과 바꿀 위치는 비교가 종료되고 나서 Pivot 이 들어갈 위치를 의미한다.
빠른 정렬은 다음과 같이 진행된다.
1. Pivot 을 정한다.
2. 배열에서 숫자들을 비교한다.
3-1. 자신보다 크면 패스한다.
3-2. 자신보다 작으면 pivot이 들어갈 위치와 자리를 바꾸고, 자리를 한 칸 옆으로 민다.
4. 비교가 종료되면 Pivot 이 들어갈 자리와 현재 Pivot 을 바꾼다.
5. 구간을 나누어 비교할 숫자가 남지 않을때까지 1~4를 반복한다.
코드는 다음과 같다.
int Sort_Quick(int * d, int order, int m, int n, int (*comp)(int x, int y))
{
// m<=x<=n까지 정렬
int temp;
// pivot =기준 idx= 비교할 숫자 t= pivot 들어갈 곳
int pivot, idx, t = m;
// 첫 요소 id가 0이면 종료
//마지막 값을 pivot 으로 지정
pivot = n;
//종료조건: 비교할 대상이 없음
if (m >= n) return 1;
//pivot 을 뺀 나머지 비교 및 스왑
for (idx = m; idx < n; idx++) {
// swap 하는 상황(오름차순 내림차순)
if (comp(d[idx], d[pivot]) != order) {
// 나보다 작은애 등장하면 내가 들어갈 위치랑 작은애가 다르면 스왑
if (t != idx) {
temp = d[idx];
d[idx] = d[t];
d[t] = temp;
}
t++;
}
}
//들어갈 위치와 pivot 바꿔줌
if (t < pivot) {
temp = d[pivot];
d[pivot] = d[t];
d[t] = temp;
}
//왼쪽
Sort_Quick(d, order, m, t - 1, comp);
//오른쪽
Sort_Quick(d, order, t + 1, n, comp);
return n - m + 1;
}만약 자신이 Quick sort를 직접 구현해서 쓸 수 있을 정도라면, C로도 무리없이 알고리즘 문제를 풀 수 있을 것이다.
나는 못할 것 같으니까 C++을 사용할까 생각중이다.
'C언어' 카테고리의 다른 글
| C++ 프로그래밍 - 표준 입출력, 이름공간(namespace), 인라인 함수(inline function), 함수 오버로딩(function overloading) (0) | 2021.05.04 |
|---|---|
| C언어의 기초 - 연결 리스트 Linked List (0) | 2021.03.04 |
| C언어의 기초 - 선행처리기 preprocessor (0) | 2021.02.07 |
| C언어의 기초 - 비트 연산자 (0) | 2021.02.06 |
| C언어의 기초 - 포인터 (0) | 2021.02.06 |